Question

Using the Factor Theorem, which of the polynomial functions has the zeros 4,
`\sqrt7`, and
`-√(7\\)`?

f (x) = x3 – 4x2 + 7x + 28
f (x) = x3 – 4x2 – 7x + 28
f (x) = x3 + 4x2 – 7x + 28
f (x) = x3 + 4x2 – 7x – 28

Answer 1

f (x) = x^3 – 4x^2 – 7x + 28

Explanation:

I got it right on the test.

Answer 2

B

Explanation:

According to the Factor Theorem, if (x - a) is a factor (where a is a zero) of the polynomial P(x), then P(a) must equal zero.

Our zeros are 4, √7, and - √7. Hence, when evaluating P(4), P(√7), and P(-√7), all must evaluate to zero.

Testing each choice, we can see that only choice B is true. That is:

`\displaystyle \displaystyle \begin{aligned} f(4)&= (4)^3 - 4(4)^2 - 7(4) + 28 \\ &= (64) - (64) - (28) + 28 \\ &= 0 \stackrel{\checkmark}{=}0 \\f(√(7)) &= (√(7))^3 - 4(√(7))^2 - 7(√(7)) + 28 \\ &= (7√(7)) - (28) - (7√(7)) + 28 \\ &= 0 \stackrel{\checkmark}{=} 0\\ f(-√(7)) &= (-√(7))^3 - 4(-√(7))^2 - 7(-√(7)) + 28 \\ &= (-7√(7)) - (28) + (7√(7)) + 28 \\ &= 0 \stackrel{\checkmark}{=} 0 \end{aligned}`

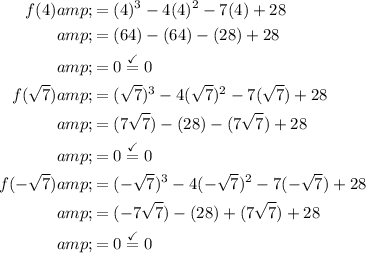
In conclusion, our answer is B.