Answer:
48
Explanation:
We are given the exponential function:—
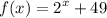
Finding average rate of change from x = 4 to x = 7:—
The formula to find average rate of change:—
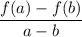 or
or
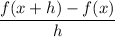
Let a be 7 and b be 4, therefore:—
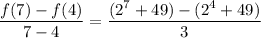
Evaluate:—
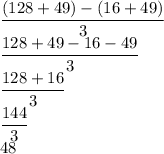
Therefore, the average of change from x = 4 to x = 7 is 48.