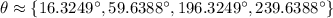Answer:
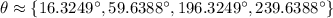
Or, their exact solutions:
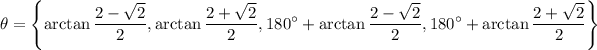
Explanation:
We want to solve the equation:
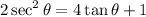
For 0° ≤ θ ≤ 360°.
Recall that tan²(θ) + 1 = sec²(θ). Substitute:
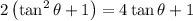
Distribute:
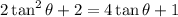
Isolate:
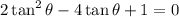
This is in quadratic form. Thus, we can solve it like a quadratic. Let u = tan(θ). Hence:
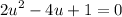
The equation is not factorable. Therefore, we can consider using the quadratic formula:
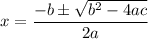
In this case, a = 2, b = -4, and c = 1. Substitute and evaluate:
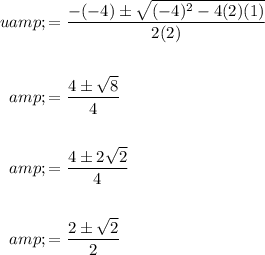
Therefore:
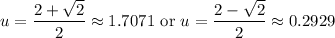
Back-substitute:
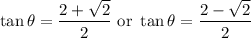
Take the inverse tangent of both equations. Hence:
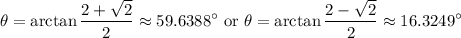
The same value of tangent occurs twice in every full rotation. Hence, by reference angles, the other two solutions are:
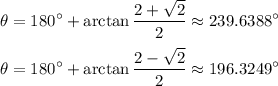
In conclusion, the four solutions are:
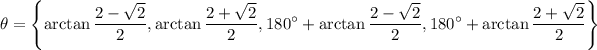 Or, approximately:
Or, approximately: