Answer:
The three even, consecutive integers are 72, 74, and 76.
Explanation:
Let a be the first even integer.
Then the other two consecutive integers, b and c, will be represented by:
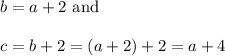
One-sixth of the smallest (that is, a) is three less than one-tenth the sum of the other two even integers (that is, b and c).
Therefore:

Solve for a. Substitute:
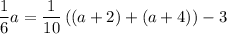
Simplify and solve for a:
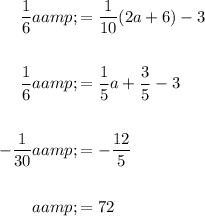
Hence, the first even integer is 72.
Therefore, the two other consecutive even integers must be 74, and 76.
In conclusion, the three even, consecutive integers are 72, 74, and 76.