Question

Anthony travels 48 miles by car in the same time it takes him to travel 12 miles on his

bike. His average rate of speed by car is 24 miles per hour faster than his average rate of speed by bike. What is the average rate of speed for both the car and the bike?

Answer 1

Anthony's average speed by car is 32 miles per hour and his average speed by bike is 8 miles per hour.

Explanation:

Let the average rate (in miles per hour) at which Anthony travels by car be c and by bike be b.

His average rate of speed by car is 24 miles per hour faster than his average rate of speed on bike. In other words:

`c = b + 24`

Anthony travels 48 miles by car in the same amount of time it takes him to travel 12 miles by bike.

Recall that distance is given by the rate multiplied by the time t.

Hence, c multiplied by time t equals 48 miles:

`\displaystyle ct = 48`

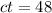
Likewise, b multiplied by the same time t equals 12 miles:

`bt = 12`

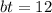
Solve. We can multiply the second equation by four:

`4bt = 48`

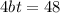
Substitute:

`ct = 4bt`

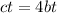
Divide:

`c = 4b`

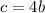
Since c = b + 24:

`(b + 24) = 4b`

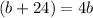
Solve for b. Subtract:

`24 = 3b`

And divide:

`b = 8\text{ miles per hour}`

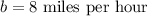
Hence, Anthony bikes at an average rate of 8 miles per hour.

Since his average speed by car is 24 miles per hour faster, his average speed by car is 32 miles per hour.

In conclusion, Anthony's average speed by car is 32 miles per hour and his average speed by bike is 8 miles per hour.