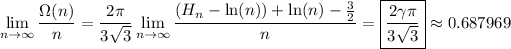Let
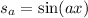 and
and
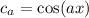 , so the integrand is
, so the integrand is
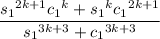
Factorize everything and recall the identities
2 s₁ c₁ = s₂
c₁² = (1 + c₂)/2
s₁² = (1 - c₂)/2
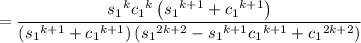
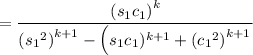
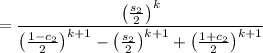
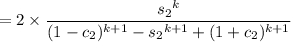
After simplifying, substitute y = 2x. Then

Now substitute t = tan(y/2). Under this change of variable, we have
dt = 1/2 sec²(y/2) dy ⇒ dy = 2/(1 + t²) dt
sin(y) = 2 sin(y/2) cos(y/2) = 2t/(1 + t²)
cos(y) = cos²(y/2) - sin²(y/2) = (1 - t²)/(1 + t²)
Making these replacements and simplifying the integrand reduces it significantly to
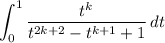
Substitute once more with z = tᵏ⁺¹ and dz = (k + 1) tᵏ dt to reduce it to the trivial
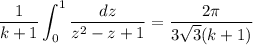
Then Ω(n) is simply
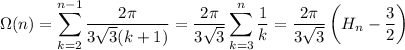
where Hₙ denotes the n-th harmonic number,
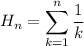
It's known that
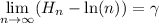
where γ ≈ 0.577216 (the Euler-Mascheroni constant). Then