Question

Integration by parts:


`\int\limits^1_ {(1)/(√(3) ) } \, arctan((1)/(x))dx`

Answer 1

The arctan function has the following property: if x is positive, then

arctan(1/x) + arctan(x) = π/2

This means

`\displaystyle \int_(1/\sqrt3)^1 \arctan\left(\frac1x\right) \, dx = \int_(1/\sqrt3)^1 \left(\frac\pi2 - \arctan(x)\right) \, dx \\\\\\ = \frac{(3-\sqrt3)\pi}6 - \int_(1/\sqrt3)^1 \arctan(x) \, dx`

For the remaining integral, integrate by parts with

`u = \arctan(x) \implies du = (dx)/(x^2+1)`

`dv = dx \implies v = x`

`\displaystyle \int_a^b \arctan(x) \, dx = uv\bigg|_a^b - \int_a^b v \, du`

`\implies \displaystyle \int_(1/\sqrt3)^1 \arctan(x) \, dx = x\arctan(x) \bigg|_(1/\sqrt3)^1 - \int_(1/\sqrt3)^1 (x)/(x^2+1) \, dx`

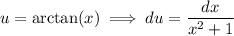
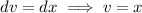
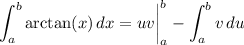
We have arctan(1) = π/4 and arctan(1/√3) = π/6, and

`\displaystyle \int (x)/(x^2+1) \, dx = \frac12 \int (d(x^2+1))/(x^2+1) = \frac12\ln(x^2+1) + C`

which gives

`\displaystyle \int_(1/\sqrt3)^1 \arctan(x) \, dx = \frac\pi4 - \frac\pi{6\sqrt3} - \frac{\ln(2) - \ln\left(\frac43\right)}2 \\\\\\ = ((9-2\sqrt3)\pi)/(36) + \frac12\ln\left(\frac23\right)`

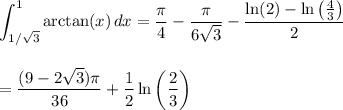
so that

`\displaystyle \int_(1/\sqrt3)^1 \arctan\left(\frac1x\right) \, dx = \frac{(3-\sqrt3)\pi}6 - ((9-2\sqrt3)\pi)/(36) - \frac12\ln\left(\frac23\right) \\\\\\ = \boxed{((9-4\sqrt3)\pi)/(36) - \frac12\ln\left(\frac23\right)}`

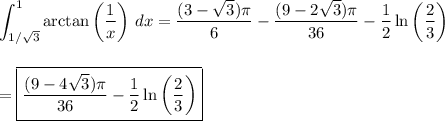
Alternatively, you can integrate by parts immediately:

`u = \arctan\left(\frac1x\right) \implies du = \frac{-\frac1{x^2}}{1+\frac1{x^2}} \, dx = -(dx)/(x^2+1)`

`dv = dx \implies v = x`

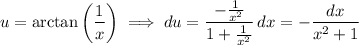
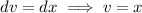
so that

`\displaystyle \int_(1/\sqrt3)^1 \arctan\left(\frac1x\right) \, dx = x\arctan\left(\frac1x\right) \bigg|_(1/\sqrt3)^1 + \int_(1/\sqrt3)^1 (x)/(x^2+1) \, dx`

You'll end up with the same result either way.