Answer:
Yes.
Explanation:
We want to determine if (x + 1) is a factor of the polynomial:
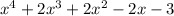
According to the Factor Theorem, if a binomial in the form (x - a) is a factor of a polynomial P(x), then P(a) must equal zero.
Our binomial factor is (x + 1) or (x - (-1)). Hence, a = -1.
Let our polynomial be P(x). Find P(-1):
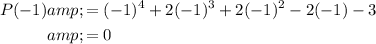
Therefore, since the resulting value is indeed zero, (x + 1) is indeed a factor of the given polynomial.
In conclusion: yes.