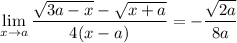Answer:
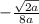
=======================================================
Step-by-step explanation:
The (x-a) in the denominator causes a problem if we tried to simply directly substitute in x = a. This is because we get a division by zero error.
The trick often used for problems like this is to rationalize the numerator as shown in the steps below.

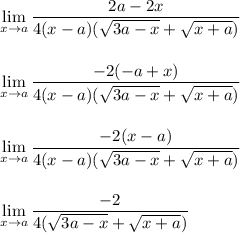
At this point, the (x-a) in the denominator has been canceled out. We can now plug in x = a to see what happens
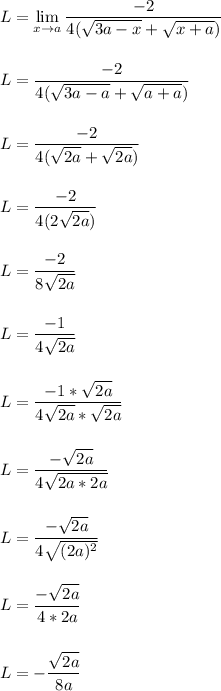
There's not much else to say from here since we don't know the value of 'a'. So we can stop here.
Therefore,