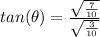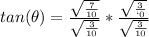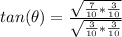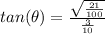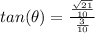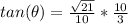Question

The angle,2Θ, lies in the third quadrant such that cos2Θ=-2/5. Determine an exact value for tanΘ . Show your work including any diagrams if you plan to use them. (3 marks)

Answer 1

`tan(\theta)=(√(21))/(3)`

Explanation:

1. Approach

One is given the following information:

`cos(2\theta)=-(2)/(5)`

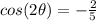
One can rewrite this as:

`cos(2\theta)=-0.4`

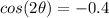
Also note, the problem says that the angle (
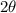`2\theta`) is found in the third quadrant.

Using the trigonometric identities (
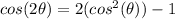`cos(2\theta)=2(cos^2(\theta))-1`) and (
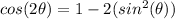`cos(2\theta)=1-2(sin^2(\theta))`) one can solve for the values of (
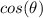`cos(\theta)`) and (
`sin(\theta)`). After doing so one can use another trigonometric identity (
`tan(\theta)=(sin(\theta))/(cos(\theta))`). Substitute the given information into the ratio and simplify.

2. Solve for
`(cos(\theta))`

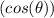
Use the following identity to solve for (
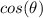`cos(\theta)`) when given the value (
`cos(2\theta)`).

`cos(2\theta)=2(cos^2(\theta))-1`

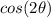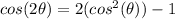
Substitute the given information in and solve for (
`cos(\theta)`).

`cos(2\theta)=2(cos^2(\theta))-1`

`-0.4=2(cos^2(\theta))-1`

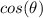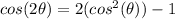
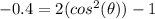
Inverse operations,

`-0.4=2(cos^2(\theta))-1`

`0.6=2(cos^2(\theta))`

`0.3=cos^2(\theta)`

`√(0.3)=cos(\theta)`

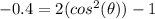
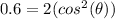
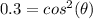
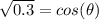
Since this angle is found in the third quadrant its value is actually:

`cos(\theta)=-√(0.3)`

3. Solve for
`(sin(\theta))`

Use the other identity to solve for the value of (
`sin(\theta)`) when given the value of (
`cos(2\theta)`).

`cos(2\theta)=1-2(sin^2(\theta))`

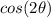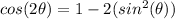
Substitute the given information in and solve for (
`sin(\theta)`).

`cos(2\theta)=1-2(sin^2(\theta))`

`-0.4=1-2(sin^2(\theta))`

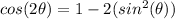
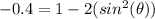
Inverse operations,

`-0.4=1-2(sin^2(\theta))`

`-1.4=-2(sin^2(\theta))`

`0.7=sin^2(\theta)`

`√(0.7)=sin(\theta)`

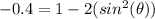
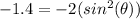
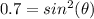
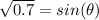
Since this angle is found in the third quadrant, its value is actually:

`sin(\theta)=-√(0.7)`

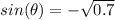
4. Solve for
`(tan(\theta))`

One can use the following identity to solve for
`(tan(\theta))`;

`tan(\theta)=(sin(\theta))/(cos(\theta))`

Substitute the values on just solved for and simplify,

`tan(\theta)=(sin(\theta))/(cos(\theta))`

`tan(\theta)=(-√(0.7))/(-√(0.3))`

`tan(\theta)=(√(0.7))/(√(0.3))`

`tan(\theta)=\frac{\sqrt{(7)/(10)}}{\sqrt{(3)/(10)}}`

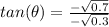
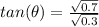
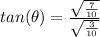
Rationalize the denominator,

`tan(\theta)=\frac{\sqrt{(7)/(10)}}{\sqrt{(3)/(10)}}`

`tan(\theta)=\frac{\sqrt{(7)/(10)}}{\sqrt{(3)/(10)}}*\frac{\sqrt{(3)/(`0)}}{\sqrt{(3)/(10)}}`

`tan(\theta)=\frac{\sqrt{(7)/(10)*(3)/(10)}}{\sqrt{(3)/(10)*(3)/(10)}}`

`tan(\theta)=\frac{\sqrt{(21)/(100)}}{(3)/(10)}`

`tan(\theta)=((√(21))/(10))/((3)/(10))`

`tan(\theta)=(√(21))/(10)*(10)/(3)`

`tan(\theta)=(√(21))/(3)`