Answer:
7.5 -ln(0.25)
Explanation:
We can first graph this function. Looking at the graph, we can separate this into two ranges -- from x=0.25 to x=1 and from x=1 to x=4.
From x=0.25 to x=1, we want to find the area above y=1/x and below y=4. To do this, we can take the integral of y=4 from x=0.25 to x=1 to encompass the whole area under y=4 from that range. Then, we subtract the area under y=1/x as we don't need that (we only want what's above it). Therefore, we have
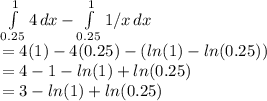
Next, we know that ln(x/y) = ln(x) - ln(y), so ln(0.25) - ln(1) = ln(0.25/1) = ln(0.25), so we have
3 - ln(0.25)
For x=1 to x=4, we want to find the area above y=x and below y=4. We can apply a similar strategy, subtracting the area below y=x from the area below y=4 to get
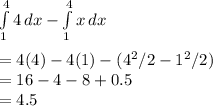
Add these two areas up to get
3-ln(0.25) + 4.5 = 7.5 -ln(0.25)