The Sequence:
1 , 1+2 , 1+2+3 , 1+2+3+4, ...
here, every term is an AP. finding the general formula for the sum of the elements of each term is:
Sₙ =
 [where x = number of term, a = first term and d = common difference]
[where x = number of term, a = first term and d = common difference]
here, the first term is always 1 and so is the common difference.
Sₙ =
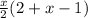
Sₙ =
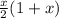 =
=
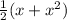
which is the formula for a general term in our series
now, we need to find the sum of the first n terms of this series
![\displaystyle\sum_(x=1)^(n) [(1)/(2)(x + x^(2))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ifu9n8cnb3be4egdctp7shf5kfstel9wt1.png)
![\displaystyle(1)/(2) [\sum_(x=1)^(n) (x) + \sum_(x=1)^(n)(x^(2))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/cigr7h6egk8fxbubaua3k7a13ueyzcnhgh.png)
in this formula, for the first term, it's just an AP from x = 1 to x = n
for the second term, we have a general formula

![(1)/(2)[(n)/(2)(2a + (n-1)d)+ (n(n+1)(2n+1))/(6) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3r6zote5q1ttn3md3kejrjeyhr2ihki67x.png)
in this AP (first term), the first term and the common difference is 1 as well
![(1)/(2)[(n)/(2)(2 + n-1)+ (n(n+1)(2n+1))/(6) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/hvo8t7j7yt9jnp8poone703rg3ayjpwxta.png)
![(1)/(2)[(n)/(2)(n+1)+ (n(n+1)(2n+1))/(6) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/omku3c4k0mq1q5dic3lq6i5kjl3kjrrkcq.png)
![[(n)/(4)(n+1)+ (n(n+1)(2n+1))/(12) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/pr54ua5joabse5b4eopfps5bb3sy44ei09.png)
![(n)/(4)(n+1) [1+((2n+1))/(3) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/b3ivpbkq4dyp2hb2mzl3iwyuksu0md5f95.png)
![(n)/(4)(n+1) [((3+2n+1))/(3) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2lkx4ud7cc6l1khtw8r12s847hx798598a.png)
![(n)/(4)(n+1) [((2n+4))/(3) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/r7bfx679a76stqdmi563bek503f95gbd1t.png)
![(n)/(2)(n+1) [((n+2))/(3) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qiqu6j9ca1xmj4yqb2uuknoojy03inigdc.png)

which is the sum of n terms of the given sequence