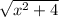Question

`(x+3).(x+2)=√(x^2+4)`

Answer 1

OK, so I thought I could solve this but now I'm not so sure. I got
`\sqrt{x^(2)+4}` =
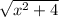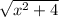`\sqrt{x^(2)+4}` but this whole thing is such a huge mess I have no idea if it's right or wrong. I tried my best to get it right and I hope this helps.

Explanation:

First, let's simplify the left side:

let's make (x + 3) = a and (x + 2) = b

so a · b or ab =

Now let's solve for a:

ab =
`\sqrt{x^(2)+4}`

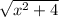
ab/b = (
`\sqrt{x^(2)+4}`) / b

a = (
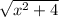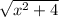`\sqrt{x^(2)+4}`) / b

Now we can substitute a:

[(
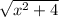`\sqrt{x^(2)+4}`) / b] · b =
`\sqrt{x^(2)+4}`

{[(
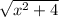
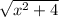`\sqrt{x^(2)+4}`) / b] · b} / [(
`\sqrt{x^(2)+4}`) / b] = (
`\sqrt{x^(2)+4}`) / [(
`\sqrt{x^(2)+4}`) / b}

b = (
`\sqrt{x^(2)+4}`) / [(
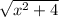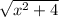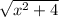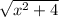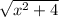`\sqrt{x^(2)+4}`) / b]

Now we can substitute a and b:

[(
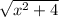`\sqrt{x^(2)+4}`) / b] · (
`\sqrt{x^(2)+4}`) / [(
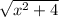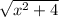`\sqrt{x^(2)+4}`) / b] =
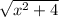
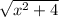`\sqrt{x^(2)+4}`

`\sqrt{x^(2)+4}` =
`\sqrt{x^(2)+4}`