Answer: (1, 2)
Concept:
There are three general ways to solve systems of equations:
- Elimination
- Substitution
- Graphing
Since the question has specific requirements, we are going to use elimination
Solve:
Given expressions
x + 5y = 11
-x + 4y = 7
Add both equations together to elimination [x] variable
(x + 5y) + (-x + 4y) = 11 + 7
x - x + 5y + 4y = 18
9y = 18
Divide 9 on both sides
9y / 9 = 18 / 9
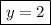
Find the x value
x + 5y = 11 ⇔ Given equation
x + 5(2) = 11 ⇔ Substitute values of y
x + 10 = 11 ⇔ Simplify by multiplication
x + 10 - 10 = 11 - 10 ⇔ Subtract 10 on both sides

Hope this helps!! :)
Please let me know if you have any questions