Answer:

Explanation:
We are asked to find the midpoint of a segment. We essentially calculate the average of the x-coordinates and the y-coordinates using the following formula.

In this formula, (x₁ , y₁) and (x₂ , y₂) are the endpoints of the segment. For this problem, the 2 endpoints are (-12, 12) and (-6, -1). If we match the variable and the corresponding value, we see that:
- x₁= -12
- y₁= 12
- x₂ = -6
- y₂ = -1
Substitute the values into the formula.
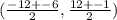
Solve the numerators.
- -12 + -6 = -12 -6 = -18
- 12 + -1 = 12-1 = 11
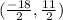
Divide.
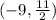
The midpoint of the segment is
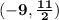 .
.