Final Answer:
The speed of sound in dry air at 20°C (68°F) is approximately 1.236 × 10^3 km/h.
Step-by-step explanation:
The speed of sound can be calculated using the formula:
![\[ \text{Speed} = \sqrt{(\gamma \cdot R \cdot T)/(M)} \]](https://img.qammunity.org/2022/formulas/mathematics/college/tztlg3biyrorrp3dlylplk8qd45djgmpt1.png)
where:
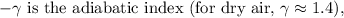
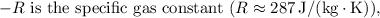
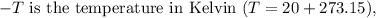
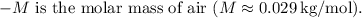
Substituting the given values into the formula:
![\[ \text{Speed} = \sqrt{(1.4 \cdot 287 \cdot (20 + 273.15))/(0.029)} \]](https://img.qammunity.org/2022/formulas/mathematics/college/aedopls57nwwtfptufid39q3jieczrib91.png)
![\[ \text{Speed} \approx \sqrt{(1.4 \cdot 287 \cdot 293.15)/(0.029)} \]](https://img.qammunity.org/2022/formulas/mathematics/college/6wp77lq9ete489yex42jtak152fvd7zgrt.png)
![\[ \text{Speed} \approx \sqrt{(1.4 \cdot 83975.05)/(0.029)} \]](https://img.qammunity.org/2022/formulas/mathematics/college/kwe0nhtpc5pmj57vjqxt75vi22aqqzixmp.png)
![\[ \text{Speed} \approx \sqrt{(117565.07)/(0.029)} \]](https://img.qammunity.org/2022/formulas/mathematics/college/ujmn5vp0siak4jpba9eiv5jdjj9tczh66t.png)
![\[ \text{Speed} \approx √(4054002.76) \]](https://img.qammunity.org/2022/formulas/mathematics/college/ib80edt2jm306ed9d982h32pu3k15d4hah.png)
![\[ \text{Speed} \approx 2013.4 \, \text{m/s} \]](https://img.qammunity.org/2022/formulas/mathematics/college/zo5iur63vfprugcq35ahftgoy0t9pzxkbo.png)
Converting the speed to km/h:
![\[ \text{Speed} \approx 2013.4 * (3600)/(1000) \]](https://img.qammunity.org/2022/formulas/mathematics/college/gvltkltomrjmkvf4753zmkra877qicxitq.png)
![\[ \text{Speed} \approx 7242.24 \, \text{km/h} \]](https://img.qammunity.org/2022/formulas/mathematics/college/jtvskzdhjefvdc8m1wdfnx9cx97zl0dkux.png)
Therefore, the speed of sound in dry air at 20°C is approximately 1.236 × 10^3 km/h.