Question

Suppose that $6500 is placed in an account that pays 11% interest compounded each year.

Assume that no withdrawals are made from the account.
Follow the instructions below. Do not do any rounding.
(a) Find the amount in the account at the end of 1 year.
se
(b) Find the amount in the account at the end of 2 years.

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Given :-

• $6500 is placed in an account that pays 11% interest compound each year
• No withdrawals are made from the account

Solution ( a)

Here, we have,

• Principal = $6500
• Time = 1 year
• Rate = 11 %

We know that, For finding amount in compound interest we use formula :-

`\bold{ A = P( 1 + }{\bold{( R)/(100)}}{\bold{)^(n)}}`

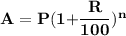
Subsitute the required values,

`\sf{ A = 6500( 1 + }{\sf{(11 )/(100)}}{\sf{)^(1)}}`

`\sf{ A = 6500( }{\sf{( 100 + 11)/(100)}}{\sf{)^(1)}}`

`\sf{ A = 6500( }{\sf{( 111)/(100)}}{\sf{)^(1)}}`

`\sf{ A = 6500 {*} }{\sf{( 111)/(100)}}`

`\sf{ A = 65 {*} 111 }`

`\bold{ A = 7215 \: dollars }`

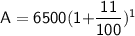
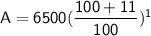
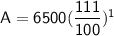
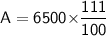
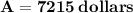
Hence, The total amount he will recieve at the end of 1 year is $7215

Solution ( b)

Here, we have,

• Principal = $6500
• Rate = 11%
• Time = 2 years

Therefore,

Amount at the end of 2 years will be

`\sf{ A = 6500( 1 + }{\sf{(11 )/(100)}}{\sf{)^(2)}}`

`\sf{ A = 6500( }{\sf{( 100 + 11)/(100)}}{\sf{)^(2)}}`

`\sf{ A = 6500( }{\sf{( 111)/(100)}}{\sf{)^(2)}}`

`\sf{ A = 6500 {*} }{\sf{( 111)/(100)}}{\sf{*{( 111)/(100)}}}`

`\sf{ A = 65 {*} 111 {*} 1.11}`

`\sf{ A = 7215 {*} 1.11 }`

`\bold{ A = 8008.65 }`

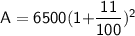
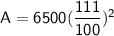
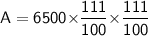
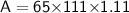
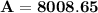
Hence, The total amount he will receive at the end of 2 years will be $8008.65