
Given :-
- Here, We have given the arithmetic sequence that is 4 , 10 , 16 , 22 ...and so on
To Find :-
- We have to find the 68th term of the given AP
Let's Begin :-
Here, we have
- Arithmetic sequence :- 4 , 10 , 16 , 22
We have to determine the 68th term of given AP
Therefore,
By using an formula that is,
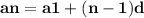
- Here, a1 = first term
- n = number of terms
- d = common difference
- an = term number
For finding common difference of AP
- Subtract preceeding term from succeeding term
- That is, a2 - a1
Here, common difference will be
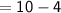
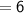
Thus, The common difference of the given AP is 6
Now, Subsitute the given values in the above an formula :-
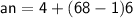
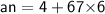
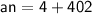
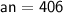
Hence, The 68th term of the given AP is 406
Some basic details about AP
- Arithmetic progression is the sequence of numbers that have same common difference between each succeeding and preceeding term.
- For finding terms,
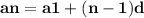
- For finding sum of terms
![\bold{\red{ sn = }}{\bold{\red{(n)/(2)}}}{\bold{\red{ [2a + ( n - 1)d ]}}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/j7depmgitgkoxcah9fo3.png)