Question

The points (a,b) and (c,d) form a segment, and the points (d,e) and (d,f) form a segment. Create an equation assuming the segments are congruent

Answer 1

If the segments are congurent they are of equal length.

So constructing an equation will not be hard.

Take for example
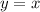`y=x` and limit x to be between and including 0 and 1 for the first segment. In this case our segment is
`(a,b)\to(c,d)=(0,0)\to(1,1)`.

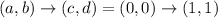Now, d has been fixated to the value of 1 and we need to construct a segment from
`(1,e)\to(1,f)`.

Since both x coordinates of the endpoints of the segment are fixed to be 1, we cannot run anymore, that is, we fixated our run. But on the rise (y-axis direction) we can still move one unit up.

Let e be 1 and f be 2. The distance between
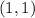`(1,1)` and
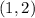`(1,2)` is 1 which is also the distance between
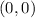`(0,0)` and
`(1,1)`.

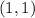Now we are asked to find the equation of both segments.

First segment is described by
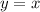`y=x` with limited domain of
`0\leq x\leq1`.

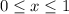Second segment is described by
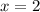`x=2` with again limited domain of
`1\leq y\leq2`.

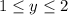Hope this helps :)