Question

Find the 68th term of the following arithmetic sequence.
4, 10, 16, 22, …

Answer 1

The given Arithmetic Sequence is 4 , 10 , 16 , 22 , ... and we need to find the 68th term of the sequence , but let's recall that for any sequence in AP , the nth term is :

• 
  `{\boxed{\bf{a_(n)=a+(n-1)d}}}`

Where ,
`\bf a` is the first term of the sequence and
`\bf d` is the common difference (
`{\bf{a_(n)-a_(n-1)}}` ) and
`\bf a_n` is nth term. So , now in this question , a = 4 and d = 10 - 4 = 6 . Now , rhe 68th term will be :

`{:\implies \quad \sf a_(68)=4+(68-1)6}`

`{:\implies \quad \sf a_(68)=4+(67)6}`

`{:\implies \quad \sf a_(68)=4+402=406}`

Hence , the 68th term is 406

Answer 2

`\bold{\huge{\underline{ Solution }}}`

Given :-

• Here, We have given the arithmetic sequence that is 4 , 10 , 16 , 22 ...and so on

To Find :-

• We have to find the 68th term of the given AP

Let's Begin :-

Here, we have

• Arithmetic sequence :- 4 , 10 , 16 , 22

We have to determine the 68th term of given AP

Therefore,

By using an formula that is,

`\bold{\red{ an = a1 + (n - 1)d }}`

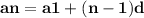
• Here, a1 = first term
• n = number of terms
• d = common difference
• an = term number

For finding common difference of AP

• Subtract preceeding term from succeeding term
• That is, a2 - a1

Here, common difference will be

`\sf{ = 10 - 4 }`

`\sf{ = 6 }`

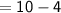
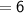
Thus, The common difference of the given AP is 6

Now, Subsitute the given values in the above an formula :-

`\sf{ an = 4 + (68 - 1)6 }`

`\sf{ an = 4 + 67 {*} 6 }`

`\sf{ an = 4 + 402 }`

`\sf{ an = 406 }`

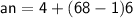
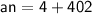
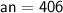
Hence, The 68th term of the given AP is 406

Some basic details about AP

• Arithmetic progression is the sequence of numbers that have same common difference between each succeeding and preceeding term.
• For finding terms,
• 
  `\bold{\red{ an = a1 + (n - 1)d }}`
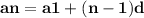
• For finding sum of terms
• 
  `\bold{\red{ sn = }}{\bold{\red{(n)/(2)}}}{\bold{\red{ [2a + ( n - 1)d ]}}}`