Question

Can someone please help me answer this function please?

Answer 1

B)
`x\geq0`

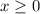
Explanation:

The domain of the square root function is all real non-negative numbers. In a numerical format that is as follows:

`D(√(x))={[0,\infty )}`

This is more commonly denoted as:

`x\geq0`

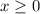
In the case of the given function:

`g(x)=√(8x)`

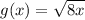
The domain is still (
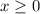`x\geq0`) as multiplying a value by (8) does not alter this. A negative number times (8) is still negative and thus cannot be a part of the square root domain. Similarly, a positive number times (8) is still positive and remains a part of the square root domain. Moreover, (0) times (8) is still (0).