1 Answer

Likan Zhan · Answer 1 · 2022-12-08T08:56:46+0000

Answer:

The area of the circle is 100 square units.

Explanation:

We are given that the circumference of a circle is 20π, and we want to determine its area.

Recall that the circumference of a circle is given by the formula:

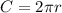
$\displaystyle C = 2\pi r$

Substitute:

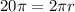
$20 \pi = 2 \pi r$

Solve for the radius:

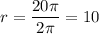
$\displaystyle r = (20\pi)/(2\pi) = 10$

The area of a circle is given by:

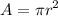
$\displaystyle A = \pi r^2$

Since the radius is 10 units:

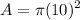
$\displaystyle A = \pi (10)^2$

Evaluate:

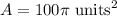
$\displaystyle A = 100\pi\text{ units}^2$

In conclusion, the area of the circle is 100 square units.

Please log in or register to add a comment.