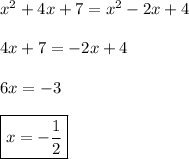\ sqrt {x ^ 2 + 4x + 7} = \ sqrt {x ^ 2-2x + 4

Question

asked Sep 12, 2022 90.6k views

1 Answer

Rsteg · Answer 1 · 2022-09-18T11:32:54+0000

First note the domain of the expressions on either side of the equation,

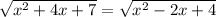
√(x^2 + 4x + 7) = √(x^2 - 2x + 4)

√x is defined only for x ≥ 0, so we need to have

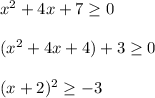
$x^2 + 4x + 7 \ge 0 \\\\ (x^2+4x+4) + 3 \ge 0 \\\\ (x+2)^2 \ge -3$

and

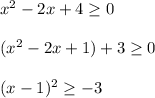
$x^2 - 2x + 4 \ge 0 \\\\ (x^2 - 2x + 1) + 3 \ge 0 \\\\ (x-1)^2 \ge -3$

but x ² ≥ 0 for all real x, so both conditions will always be satisfied.

Back to the equation - take the square of both sides and solve for x :

$x^2 + 4x + 7 = x^2 - 2x + 4 \\\\ 4x + 7 = -2x + 4 \\\\ 6x = -3 \\\\ \boxed{x=-\frac12}$