Answer:

Explanation:
we would like to evaluate the following sum of geometric series:
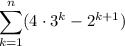
to do so recall the Substracting property of partial sum Thus,
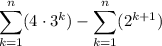
rewrite $2^{k+1}$ as 2•2^k:
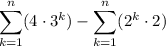
utilize constant property of partial sum:
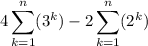
factor out 2:
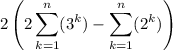
calculate the sum:
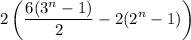
distribute:
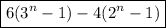
and we're done: