Answer:
The value of x is 6.
Step-by-step explanation:
Question :
The perimeter of an equilateral triangle is 63 inches. If the length lf each side is (4x - 3), find the value of x.

Solution :
As we know that the formula of perimeter of equilateral triangle is 3a.
Now, according to the question :


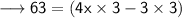
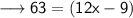
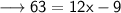

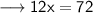
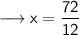
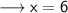

Hence, the value of x is 6.
