Question

Which of the following graphs shows the solution set for the inequality below? 3|x + 1| < 9

Answer 1

Explanation:

The absolute value function is a well known piecewise function (a function defined by multiple subfunctions) that is described mathematically as

`f(x) \ = \ |x| \ = \ \left\{\left\begin{array}{ccc}x, \ \text{if} \ x \ \geq \ 0 \\ \\ -x, \ \text{if} \ x \ < \ 0\end{array}\right\}`.

This definition of the absolute function can be explained geometrically to be similar to the straight line
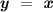`\textbf{\textit{y}} \ = \ \textbf{\textit{x}}` , however, when the value of x is negative, the range of the function remains positive. In other words, the segment of the line
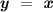`\textbf{\textit{y}} \ = \ \textbf{\textit{x}}` where
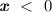`\textbf{\textit{x}} \ < \ 0` (shown as the orange dotted line), the segment of the line is reflected across the x-axis.

First, we simplify the expression.

`3\left|x \ + \ 1 \right| \ < \ 9 \\ \\ \\\-\hspace{0.2cm} \left|x \ + \ 1 \right| \ < \ 3`.

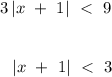We, now, can simply visualise the straight line,
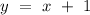`y \ = \ x \ + \ 1` , as a line having its y-intercept at the point
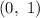`(0, \ 1)` and its x-intercept at the point
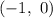`(-1, \ 0)`. Then, imagine that the segment of the line where
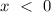`x \ < \ 0` to be reflected along the x-axis, and you get the graph of the absolute function
`y \ = \ \left|x \ + \ 1 \right|`.

Consider the inequality

`\left|x \ + \ 1 \right| \ < \ 3`,

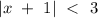this statement can actually be conceptualise as the question

```\text{For what \textbf{values of \textit{x}} will the absolute function \textbf{be less than 3}}`.

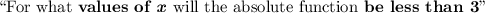Algebraically, we can solve this inequality by breaking the function into two different subfunctions (according to the definition above).

• Case 1 (when
  `x \ \geq \ 0`)

`x \ + \ 1 \ < \ 3 \\ \\ \\ \-\hspace{0.9cm} x \ < \ 3 \ - \ 1 \\ \\ \\ \-\hspace{0.9cm} x \ < \ 2`

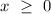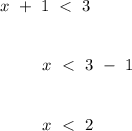
• Case 2 (when
  `x \ < \ 0`)

`-(x \ + \ 1) \ < \ 3 \\ \\ \\ \-\hspace{0.15cm} -x \ - \ 1 \ < \ 3 \\ \\ \\ \-\hspace{1cm} -x \ < \ 3 \ + \ 1 \\ \\ \\ \-\hspace{1cm} -x \ < \ 4 \\ \\ \\ \-\hspace{1.5cm} x \ > \ -4`

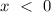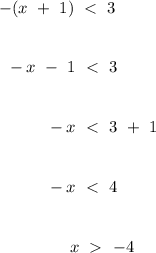
*remember to flip the inequality sign when multiplying or dividing by

negative numbers on both sides of the statement.

Therefore, the values of x that satisfy this inequality lie within the interval

`-4 \ < \ x \ < \ 2`.

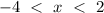Similarly, on the real number line, the interval is shown below.

The use of open circles (as in the graph) indicates that the interval highlighted on the number line does not include its boundary value (-4 and 2) since the inequality is expressed as "less than", but not "less than or equal to". Contrastingly, close circles (circles that are coloured) show the inclusivity of the boundary values of the inequality.