Question

The equation of a circle is given below. Identify the center and radius. Then graph the circle.

(x-3)² + y² =9

Answer 1

(x－3)²＋y²＝9
(x－3)²＋(y－0)²＝3²
The equation can be written in the form (x－p)²＋(y－q)²＝r², so it represents a circle with the radius r＝3 and the center (3, 0)

Hope my answer helped u :)

Answer 2

• Center = (3, 0)
• Radius = 3
• Graph = see below

Concept:

Here, we need to know the idea of the circle equation.

Circle equation: (x - h)² + (y - k)² = r²

(h, k) = center

r = radius

x = variable

y = variable

Solve:

Given expression

(x - 3)² + y² = 9

Find the point of the center

(h, k) =
`\boxed{(3,0)}`

Find the length of the radius

r² = 9

`\boxed{r=3}`

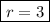
Hope this helps!! :)

Please let me know if you have any questions