Question

The sum of 30 terms of series in A.P, whose last term is 98, is 1635. Find the first term and the common difference.​

Answer 1

Let a(n) denote the n-th term in the sequence. Because the terms are in arithmetic progression, there is a fixed number d that separates consecutive terms, so that starting with a(1) = a, the next few terms are

a(2) = a(1) + d = a + d

a(3) = a(2) + d = a + 2d

a(4) = a(3) + d = a + 3d

and so on, up to

a(n) = a + (n - 1) d

We're given that the 30th term is 98, so

a(30) = a + 29d = 98

The sum of the first 30 terms is 1635, so that

`\displaystyle \sum_(n=1)^(30)a(n) = \sum_(n=1)^(30)(a+(n-1)d) \\\\ 1635 = a\sum_(n=1)^(30)1 + d\sum_(n=1)^(30)(n-1) \\\\ 1635 = 30a + d\sum_(n=0)^(29)n \\\\ 1635 = 30a + d\sum_(n=1)^(29)n \\\\ 1635 = 30a + \frac{d*29*30}2`

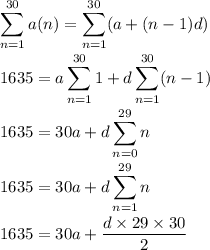
so that

30a + 435d = 1635

Solve the equations in boldface for a and d. I'll eliminate a and solve for d first.

-30 (a + 29d) + (30a + 435d) = -30 (98) + 1635

-30a - 870d + 30a + 435d = -2940 + 1635

-435d = -1305

d = 3

Then

a + 29 (3) = 98

a + 87 = 98

a = 11