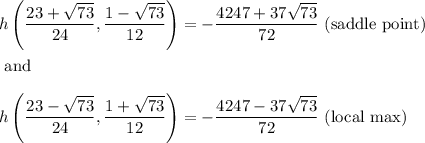Question

Let the (x; y) coordinates represent locations on the ground. The height h of

a particle is governed by the function described below. Classify all the critical
points of height and find the value(s) of height h at those points.
h(x; y) = 8x + 10y - 4xy - 4x^2 - 4y^3

Answer 1

The critical points of h(x,y) occur wherever its partial derivatives
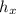`h_x` and
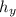`h_y` vanish simultaneously. We have

`h_x = 8-4y-8x = 0 \implies y=2-2x \\\\ h_y = 10-4x-12y^2 = 0 \implies 2x+6y^2=5`

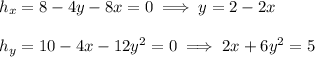
Substitute y in the second equation and solve for x, then for y :

`2x+6(2-2x)^2=5 \\\\ 24x^2-46x+19=0 \\\\ \implies x=(23\pm√(73))/(24)\text{ and }y=(1\mp√(73))/(12)`

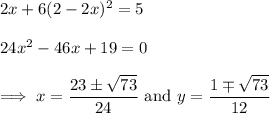
This is to say there are two critical points,

`(x,y)=\left((23+√(73))/(24),(1-√(73))/(12)\right)\text{ and }(x,y)=\left((23-√(73))/(24),(1+√(73))/(12)\right)`

To classify these critical points, we carry out the second partial derivative test. h(x,y) has Hessian

`H(x,y) = \begin{bmatrix}h_(xx)&h_(xy)\\h_(yx)&h_(yy)\end{bmatrix} = \begin{bmatrix}-8&-4\\-4&-24y\end{bmatrix}`

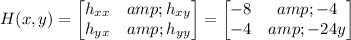
whose determinant is
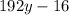`192y-16`. Now,

• if the Hessian determinant is negative at a given critical point, then you have a saddle point

• if both the determinant and
`h_(xx)` are positive at the point, then it's a local minimum

• if the determinant is positive and
`h_(xx)` is negative, then it's a local maximum

• otherwise the test fails

We have

`\det\left(H\left((23+√(73))/(24),(1-√(73))/(12)\right)\right) = -16√(73) < 0`

while

`\det\left(H\left((23-√(73))/(24),(1+√(73))/(12)\right)\right) = 16√(73)>0 \\\\ \text{ and } \\\\ h_(xx)\left((23+√(73))/(24),(1-√(73))/(12)\right)=-8 < 0`

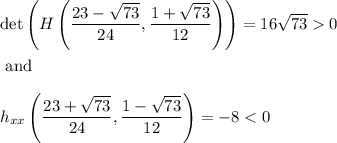
So, we end up with

`h\left((23+√(73))/(24),(1-√(73))/(12)\right)=-(4247+37√(73))/(72) \text{ (saddle point)}\\\\\text{ and }\\\\h\left((23-√(73))/(24),(1+√(73))/(12)\right)=-(4247-37√(73))/(72) \text{ (local max)}`