Question

Find the point on the paraboloid z = 4x2 + 4y2 which is closest to the point
(4; 5; 6).

Answer 1

Using the method of Lagrange multipliers: the Lagrangian is

`L(x,y,z,\lambda) = (x-4)^2+(y-5)^2+(z-6)^2 - \lambda (z-4x^2-4y^2)`

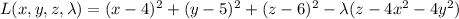
Fix λ > 0.

That is, we are minimizing the squared distance of a point (x, y, z) on the paraboloid to the point (4, 5, 6). We can use the squared distance in place of the proper Euclidean distance because both f(x) and √f(x) have critical points at the same point x ; plus the math works out much more easily.

Find the critical points of the Lagrangian:

`(\partial L)/(\partial x) = 2(x-4) + 8\lambda x = 0 \\\\ (\partial L)/(\partial y) = 2(y-5) + 8\lambda y = 0 \\\\ (\partial L)/(\partial z) = 2(z-6) - \lambda = 0 \\\\ (\partial L)/(\partial\lambda) = -z+4x^2+4y^2 = 0`

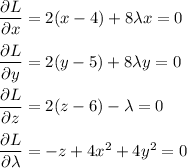
Solving for λ in terms of x, y, or z gives

`\displaystyle \lambda = \frac1x-\frac14 = \frac5{4y} - \frac14 = 2z-12`

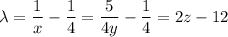
so right away, we get

`\frac5{4y} - \frac14 = \frac1x - \frac14 \implies y=\frac{5x}4 \\\\ 2z-12 = \frac1x-\frac14 \implies z = \frac1{2x} + \frac{47}8`

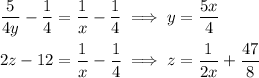
Substitute these into the constraint and solve for x, then for y and z :

`\frac1{2x} + \frac{47}8 = 4x^2 +4\left(\frac{5x}4\right)^2 \implies 82x^3 - 47x - 4 = 0`

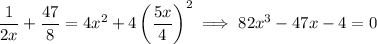
This has 3 roots, but we take the lone positive solution for x because otherwise λ would be negative. This root is x ≈ 0.7965.

Then it follows that the closest point on the paraboloid to (4, 5, 6) is the critical point (0.7965, 0.9956, 6.5028).