Question

W(x) = x2 + 1; Find w(x + 3)

Answer 1

Given the function w:

`\displaystyle \large{w(x) = {x}^(2) + 1 }`

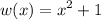
Since we want to find w(x+3), the input would be x+3.

Substitute x = x+3 in.

`\displaystyle \large{w(x + 3) = {(x + 3)}^(2) + 1 }`

Alternate Solution

The answer above works if you want it in vertex form. For this alternate solution, I will convert the function in standard form.

As we know:

`\displaystyle \large{ {(x + y)}^(2) = {x}^(2) + 2xy + {y}^(2) }`

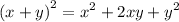
Therefore:

`\displaystyle \large{ {(x + 3)}^(2) = {x}^(2) + 2(x)(3) + {3}^(2) } \\ \displaystyle \large{ {(x + 3)}^(2) = {x}^(2) + 6x+ 9}`

Now for function w:

`\displaystyle \large{w(x + 3) = {x}^(2) + 6x + 9+ 1 } \\ \displaystyle \large{w(x + 3) = {x}^(2) + 6x + 10}`

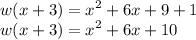
Hence:

• The answer is w(x+3) = (x+3)^2+1 for vertex form
• OR w(x+3) = x^2+6x+10