Answer:
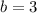
Explanation:
We are given that:

And we want to determine the value of b.
First, expand:

Therefore, we can write that:
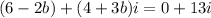
If two complex numbers are equivalent, their real and imaginary parts must be equivalent. Hence:
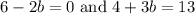
Solve for each case:

The two solutions are equivalent, hence such a number b exists.
In conclusion, b = 3.