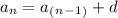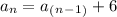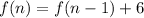Answer:
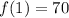
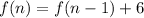
Explanation:
One is given the following function:
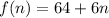
One is asked to evaluate the function for
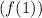 , substitute
, substitute
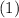 in place of
in place of
 , and simplify to evaluate:
, and simplify to evaluate:

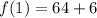
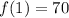
A recursive formula is another method used to represent the formula of a sequence such that each term is expressed as a function of the last term in the sequence. In this case, one is asked to find the recursive formula of an arithmetic sequence: that is, a sequence of numbers where the difference between any two consecutive terms is constant. The following general formula is used to represent the recursive formula of an arithmetic sequence:
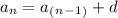
Where (
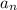 ) is the evaluator term (
) is the evaluator term (
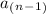 ) represents the term before the evaluator term, and (d) represents the common difference (the result attained from subtracting two consecutive terms). In this case (and in the case for most arithmetic sequences), the common difference can be found in the standard formula of the function. It is the coefficient of the variable (n) or the input variable. Substitute this into the recursive formula, then rewrite the recursive formula such that it suits the needs of the given problem,
) represents the term before the evaluator term, and (d) represents the common difference (the result attained from subtracting two consecutive terms). In this case (and in the case for most arithmetic sequences), the common difference can be found in the standard formula of the function. It is the coefficient of the variable (n) or the input variable. Substitute this into the recursive formula, then rewrite the recursive formula such that it suits the needs of the given problem,