Question

Find the equation of the line that

is parallel to y = 4x + 1 and
contains the point (1, 1).
y = [? ]X + [ ]

Answer 1

The equation of a line is:

`\displaystyle \large{y - y_1 = m(x - x_1)}`

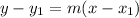
Since the line has to be parallel to line y = 4x+1. Hence, m = 4.

`\displaystyle \large{y - y_1 = 4(x - x_1)}`

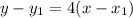
Given point is (1,1). Let this be the following:

`\displaystyle \large{(x_1,y_1) = (1,1)}`

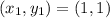
Substitute the point in.

`\displaystyle \large{y - 1 = 4(x - 1)}`

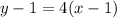
Convert the equation in a slope-intercept form or function form.

First, distribute 4 in the expression.

`\displaystyle \large{y - 1 = 4x - 4}`

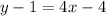
Add 1 on both sides.

`\displaystyle \large{y - 1 + 1 = 4x - 4 + 1} \\ \displaystyle \large{y = 4x - 3}`

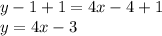
Hence, the line that is parallel to y = 4x+1 and passes through (1,1) is y = 4x-3