Question

The common ratio of the geometric sequence -14,-84,-504

Answer 1

A common ratio is basically a ratio of next sequence and the sequence you want

To find a common ratio of geometric sequence, we usually define 'r' as common ratio.

`\displaystyle \large \tt{r = (next \: \: sequence)/(the \: \: sequence \: \: you \: \: want) }`

For example, I want to focus on -14 and the next sequence would be -84.

Hence,

`\displaystyle \large{r = ( - 84)/( - 14) }`

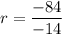
Thus, r is 6 because both numerator and denominator are negative. negative divides negative = positive.

Or you want to choose -84, then the next sequence would be -504.

`\displaystyle \large{r = ( - 504)/( - 84) }`

Then r would still be 6. Since both ways have r as 6 and this proves that the sequence is geometric.

Hence, the common ratio is 6.