Answer: (60/13, 6/13)
Concept:
There are three general ways to solve systems of equations:
- Elimination
- Substitution
- Graphing
Here, we are going to use elimination since all the variables are in the corresponding position.
Solve:
Given
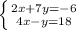
Multiply the first equation in order to eliminate [x]
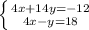
Subtract the second equation from the first equation to eliminate [x]
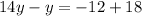
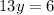
Divide 13 on both sides
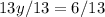
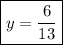
Substitute [y] value in order to get [x] value
4x - y = 18
4x - 6/13 = 18
4x = 18 + 6/13
4x = 240/13
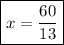
Hope this helps!! :)
Please let me know if you have any questions