Question

Find mZWVT.

T
U
7x +11)
V
(14x+7)
(3x + 4)º
W
A. 40
OB. 53
OC.50
OD. 45

Answer 1

`\huge\boxed{\sf <WVT = 40\°}`

Explanation:

According to one of the tangent-secant theorems,

∠WVT =
`(1)/(2) (arc\ TW-arc\ UW)`

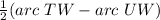
Given that:

∠WVT = (3x + 4)°

arc TW = (14x + 7)°

arc UW = (7x + 11)°

Solution:

3x + 4 = 1/2 (14x + 7 - (7x + 11))

3x + 4 = 1/2 (14x + 7 - 7x - 11)

3x + 4 = 1/2 ( 7x - 4 )

Multiply both sides by 2

2 ( 3x + 4 ) = 7x - 4

6x + 8 = 7x - 4

Combining like terms

7x - 6x = 8 + 4

x = 12

Finding ∠WVT:

∠WVT = (3x + 4)°

∠WVT = (3(12)+4)°

∠WVT = (36+4)°

∠WVT = 40°

`\rule[225]{225}{2}`

Hope this helped!

~AH1807

Peace!