Explanation:
In statistics, the empirical rule states that for a normally distributed random variable,
- 68.27% of the data lies within one standard deviation of the mean.
- 95.45% of the data lies within two standard deviations of the mean.
- 99.73% of the data lies within three standard deviations of the mean.
In mathematical notation, as shown in the figure below (for a standard normal distribution), the empirical rule is described as
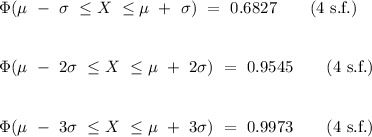
where the symbol
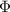 (the uppercase greek alphabet phi) is the cumulative density function of the normal distribution,
(the uppercase greek alphabet phi) is the cumulative density function of the normal distribution,
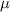 is the mean and
is the mean and
 is the standard deviation of the normal distribution defined as
is the standard deviation of the normal distribution defined as
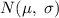 .
.
According to the empirical rule stated above, the interval that contains the prices of 99.7% of college textbooks for a normal distribution
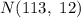 ,
,
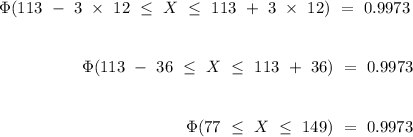
Therefore, the price of 99.7% of college textbooks falls inclusively between $77 and $149.