Question

The prices of all college textbooks follow a bell-shaped distribution with a mean of $113 and a standard deviation of $12. Using the empirical rule, find the interval that contains the prices of 99.7% of college textbooks.

Answer 1

Explanation:

In statistics, the empirical rule states that for a normally distributed random variable,

• 68.27% of the data lies within one standard deviation of the mean.

• 95.45% of the data lies within two standard deviations of the mean.

• 99.73% of the data lies within three standard deviations of the mean.

In mathematical notation, as shown in the figure below (for a standard normal distribution), the empirical rule is described as

`\Phi(\mu \ - \ \sigma \ \leq X \ \leq \mu \ + \ \sigma) \ = \ 0.6827 \qquad (4 \ \text{s.f.}) \\ \\ \\ \Phi(\mu \ - \ 2\sigma \ \leq X \ \leq \mu \ + \ 2\sigma) \ = \ 0.9545 \qquad (4 \ \text{s.f.}) \\ \\ \\ \Phi}(\mu \ - \ 3\sigma \ \leq X \ \leq \mu \ + \ 3\sigma) \ = \ 0.9973 \qquad (4 \ \text{s.f.})`

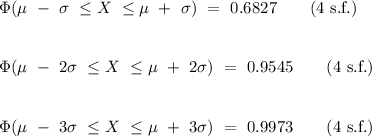
where the symbol
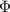`\Phi` (the uppercase greek alphabet phi) is the cumulative density function of the normal distribution,
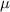`\mu` is the mean and
`\sigma` is the standard deviation of the normal distribution defined as
`N(\mu, \ \sigma)`.

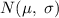According to the empirical rule stated above, the interval that contains the prices of 99.7% of college textbooks for a normal distribution
`N(113, \ 12)`,

`\Phi(113 \ - \ 3 \ * \ 12 \ \leq \ X \ \leq \ 113 \ + \ 3 \ * \ 12) \ = \ 0.9973 \\ \\ \\ \-\hspace{1.75cm} \Phi(113 \ - \ 36 \ \leq \ X \ \leq \ 113 \ + \ 36) \ = \ 0.9973 \\ \\ \\ \-\hspace{3.95cm} \Phi(77 \ \leq \ X \ \leq \ 149) \ = \ 0.9973`

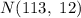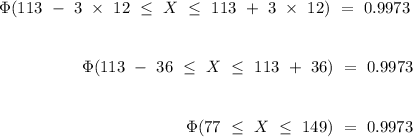
Therefore, the price of 99.7% of college textbooks falls inclusively between $77 and $149.