Answer:
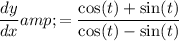 given that
given that
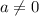 and that
and that
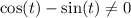 .
.
Explanation:
The relation between the
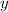 and the
and the
 in this question is given by parametric equations (with
in this question is given by parametric equations (with
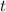 as the parameter.)
as the parameter.)
Make use of the fact that:
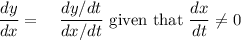 .
.
Find
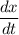 and
and
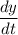 as follows:
as follows:
![\begin{aligned} (dx)/(dt) &= (d)/(dt) [a\, (\cos(t) + \sin(t))] \\ &= a\, (-\sin(t) + \cos(t)) \\ &= a\, (\cos(t) - \sin(t))\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/5fjdqltrz0dg1qxxjj835fffgsw4mtxfum.png) .
.
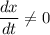 as long as
as long as
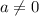 and
and
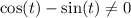 .
.
![\begin{aligned} (dy)/(dt) &= (d)/(dt) [a\, (\sin(t) - \cos(t))] \\ &= a\, (\cos(t) - (-\sin(t))) \\ &= a\, (\cos(t) + \sin(t))\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/d17w4jut40l37mihi311yqwgljpfj49m6o.png) .
.
Calculate
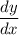 using the fact that
using the fact that
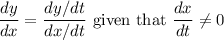 . Assume that
. Assume that
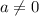 and
and
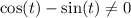 :
:
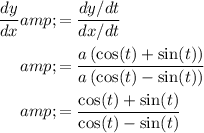 .
.