Question

19. The product of two numbers is 120 and the sum of their squares is 289. The sum of the number is (a) 20 (b) 23 (c) 169 (d) None of these​

Answer 1

B

Explanation:

Let the two numbers be a and b.

The product of the two is 120 and their sum of their squares is 289. In other words:

`\displaystyle ab = 120 \text{ and } a^2 + b^2 = 289`

And we want to find the sum of the two numbers.

We can use the perfect square trinomial. Recall that:

`a^2 + 2ab + b^2 = (a+b)^2`

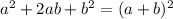
From the first equation, multiply by two:

`2ab = 240`

Add the two equations together:

`(a^2+b^2)+(2ab) = (289)+(240)`

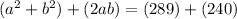
Simplify and rewrite:

`a^2+2ab+b^2 = 529`

Factor using the perfect square trinomial pattern:

`(a+b)^2 = 529`

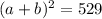
And take the square root of both sides:

`\displaystyle a + b = \pm√(529) = \pm23`

Hence, the sum of the two numbers is 23 or -23.

In conclusion, our answer is B.