Answer:

Step-by-step explanation:
We are asked to find how many moles of methane (CH₄) a cow produces in a year. We must convert molecules of methane to moles of methane. We will do this using Avogadro's Number or 6.022 × 10²³. This is the number of particles (atoms, molecules, formula units, etc.) in 1 mole of a substance.
In this case, the particles are molecules of methane. There are 6.022 × 10²³ molecules of methane in 1 mole.
We will convert molecules to moles using dimensional analysis. Set up a ratio using Avogadro's Number.

We are converting 3.571 × 10²⁷ molecules of methane to moles, so we multiply the ratio by this value.
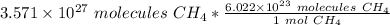
Flip the ratio. It is still the same value, but the units of molecules of methane cancel.
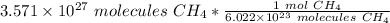
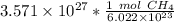
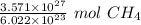

The original measurement of molecules of methane( 3.571 × 10²⁷ molecules) has 4 significant figures, so our answer must have the same. For the number we calculated, that is the ones place. The 9 in the tenth place tells us to round the 9 in the ones place up to a 0, then the 2 in the tens place up to a 3.
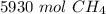
We must add a placeholder zero in the tenth place to reach 4 sig figs.
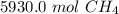
The adult cow produces approximately 5930.0 moles of methane in a year.