Answer:

Step-by-step explanation:
We are asked to find the gas pressure when the temperature of a gas is changed. We will use Gay-Lussac's Law, which states the pressure of a gas is proportional to the temperature of the gas. The formula for this law is:
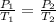
Initially, the pressure is 177 atmospheres and the temperature is 25 degrees Celsius or 298 Kelvin.
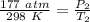
Then, the gas cylinder is exposed to fire and the temperature is raised to 195 degrees Celsius or 468 Kelvin, but the pressure is unknown.

We are solving for the new pressure, so we must isolate the variable P₂. It is being divided by 468 Kelvin. The inverse operation of division is multiplication, so we multiply both sides of the equation by 468 Kelvin.
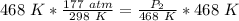
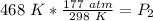
The units of Kelvin cancel.


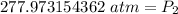
The pressure in the cylinder after exposure to fire is approximately 278 atmospheres.