Hey there! I'm happy to help!
Imagine the line that is created when you connect the two points (the distance between the two points).
You can create a right triangle where this distance is the hypotenuse where the two legs are the change in x and y. So, if you take those changes in x and y, you can use the Pythagorean Theorem (a²+b²=c²) to find the distance between the two points, which is the hypotenuse.
Our change in x is 9 because 9-0 is 9.
We square it
9²=81
Our change in y is 5 as -1-(-6) or -1+6 is 5.
5²=25
We add these.
81+25=106
We square root and round to the nearest tenth.
√106≈10.3
So, our distance is 10.3.
This Pythagorean Theorem method actually gives us a formula called the distance formula that you can use to find the distance between points.
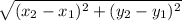
Have a wonderful day and keep on learning! :D