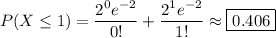A
(a) You're looking for

where
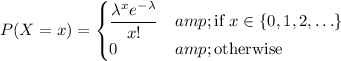
Customers arrive at a mean rate of 6 customers per 10 minutes, or equivalently 12 customers per 20 minutes, so

Then
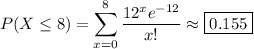
(b) Now you want
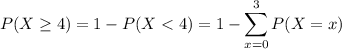
This time, we have
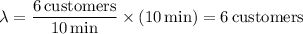
so that
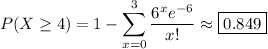
B
(a) In other words, you're asked to find the probability that more than 1 customer shows up in the same minute, or
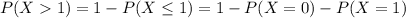
with
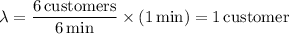
So we have
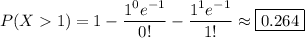
C
(a) Similar to B, you're looking for
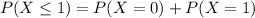
with
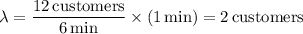
so that