Answer:
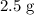 of
of
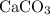 would contain:
would contain:
- Approximately
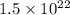 calcium atoms (approximately
calcium atoms (approximately
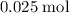 ,)
,) - Approximately
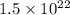 carbon atoms (approximately
carbon atoms (approximately
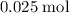 ,) and
,) and - Approximately
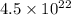 oxygen atoms (approximately
oxygen atoms (approximately
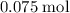 .)
.)
Step-by-step explanation:
Look up the Avogadro constant:
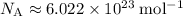 .
.
For example, "
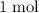 of carbon atoms" would contain
of carbon atoms" would contain
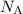 carbon atoms (approximately
carbon atoms (approximately
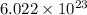 ) by definition.
) by definition.
Look up the relative atomic mass of carbon, calcium, and oxygen on a modern periodic table:
- Calcium:
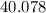 .
. - Carbon:
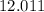 .
. - Oxygen:
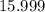 .
.
In other words, the mass of
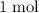 of calcium atoms would be
of calcium atoms would be
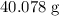 . The mass of
. The mass of
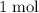 of carbon atoms would be
of carbon atoms would be
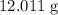 , and the mass of
, and the mass of
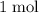 of oxygen atoms would be
of oxygen atoms would be
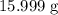 .
.
As the formula
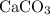 suggests, every formula unit of this ionic compound includes one calcium atom, one carbon atom, and three oxygen atoms. The formula mass of
suggests, every formula unit of this ionic compound includes one calcium atom, one carbon atom, and three oxygen atoms. The formula mass of
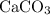 would give the mass of every mole of
would give the mass of every mole of
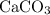 formula units.
formula units.
Calculate the formula mass of
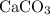 from the relative atomic mass data:
from the relative atomic mass data:
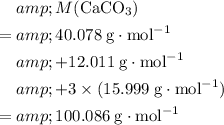 .
.
Calculate the number of
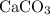 formula units in that
formula units in that
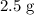 of this compound:
of this compound:
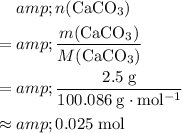 .
.
In other words,
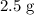 of
of
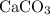 would contain approximately
would contain approximately
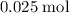
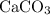 formula units.
formula units.
Again, there are one calcium atom, one carbon atom, and one oxygen atom in every
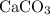 formula unit. That approximately
formula unit. That approximately
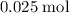
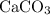 formula units would thus contain:
formula units would thus contain:
- Approximately
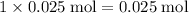 calcium atoms,
calcium atoms, - Approximately
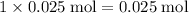 carbon atoms, and
carbon atoms, and - Approximately
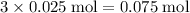 oxygen atoms.
oxygen atoms.
Make use of the Avogadro constant to convert the numbers.
For example, the number of calcium atoms in that approximately
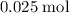 of calcium atoms would be:
of calcium atoms would be:
 .
.
Likewise, the number of carbon atoms in that approximately
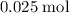 of carbon atoms would be:
of carbon atoms would be:
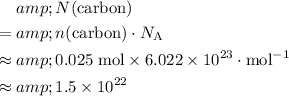 .
.
The number of oxygen atoms in that approximately
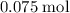 of oxygen atoms would be:
of oxygen atoms would be:
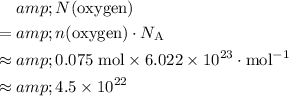 .
.