Question

Really need to someone to break this down so I can understand it

(a) Find the slope of the curve y= x^2 - 2x - 3 at the point ​P(2,​ -3​) by finding the limit of the secant slopes through point P.
(b) Find an equation of the tangent line to the curve at P(2, -3)

Answer 1

Part A)

The slope is two.

Part B)

`\displaystyle y = 2x - 7`

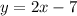
Explanation:

Part A)

We want to find the slope of the curve:

`\displaystyle y = x^2 - 2x - 3`

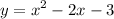
At the point P(2, -3) by using the limit of the secant slopes through point P.

To find the limit of the secant slopes, we can use the difference quotient. Recall that:

`\displaystyle f'(x) = \lim_(h \to 0) (f(x+h) - f(x))/(h)`

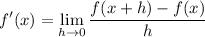
Since we want to find the slope of the curve at P(2, -3), x = 2.

Substitute:

`\displaystyle f'(2) = \lim_(h \to 0) (f(2 + h) - f(2))/(h)`

Simplify. Note that f(2) = -3. Hence:

`\displaystyle \begin{aligned} f'(2) &= \lim_(h\to 0) (\left[(2+h)^2 - 2(2+h) - 3\right] - \left[-3\right])/(h) \\ \\ &=\lim_(h \to 0)((4 + 4h + h^2)+(-4-2h)+(0))/(h) \\ \\ &= \lim_(h\to 0) (h^2+2h)/(h)\\ \\&=\lim_(h\to 0) h + 2 \\ \\ &= (0) + 2 \\ &= 2\end{aligned}`

(Note: I evaluated the limit using direct substitution.)

Hence, the slope of the curve at the point P(2, -3) is two.

Part B)

Since the slope of the curve at point P is two, the slope of the tangent line is also two.

And since we know it passes through the point (2, -3), we can consider using the point-slope form:

`\displaystyle y - y_1 = m(x-x_1)`

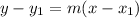
Substitute. m = 2. Therefore, our equation is:

`\displaystyle y + 3 = 2(x-2)`

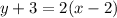
We can rewrite this into slope-intercept if desired:

`\displaystyle y = 2x - 7`

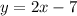
We can verify this by graphing. This is shown below: