Answer:
There are 12 horses and 18 geese.
Explanation:
We are given that in a field full of horses and geese, a farmer notes that there are 30 heads and 84 feet.
We can write a system of equations using the given information.
Let the amount of horses there are be represented by h and geese by g.
Assuming each horse and geese has only one head, we can write that:
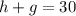
And assuming that each horse has four feet and each geese has two feet, we can write that:
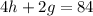
This yields a system of equations:
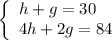
We can solve it using substitution. From the first equation, isolate either variable:
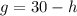
From the second, we can first divide by two:
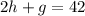
And substitute:
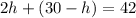
Combine like terms:
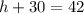
Subtract:
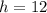
Therefore, there are 12 horses.
And since the total number of animals is 30, there must be 30 - 12 or 18 geese.
In conclusion, there are 12 horses and 18 geese.