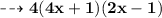Factorisation of a quadratic polynomial of the type ax² + bx + c where (a ≠ 1) .
- To factorise ax² + bx + c, we have to find two numbers whose sum is equal to the coefficient of x and product is equal to the coefficient of x² and constant term.
Now,
Solution (1) :
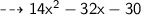

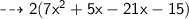
![{ \qquad \sf { \dashrightarrow{ 2[x(7x + 5) - 3(7x + 5)] }}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/r5s62h38ygr4mu41q0up4d07egti5qe3b0.png)
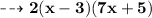
⠀
Solution (2) :
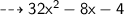
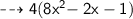
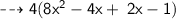
![{ \qquad \sf { \dashrightarrow{ 4[4x(2x-1) +1(2x-1)] }}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/m0smogmqhxr03193qi6ffxj0m6j7v4232e.png)