Answer:
Area of shaded region = 254.5 square units
Explanation:
We have 3 semicircles:
d = 18 units
Semicircle 1 = The big semicircle
Semicircle 2 and 3 = The two small semicircles
Semicircle 2 = 18 units
Semicircle 3 = 18 units
Semicircle 1 = Semicircle 2 + Semicircle 3 = 36 units
Radius = Half of the diameter
Semicircle 1 radius = 18 units
Semicircle 2 radius = 9 units
Semicircle 3 radius = 9 units
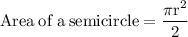

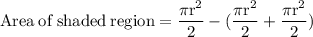
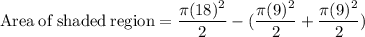
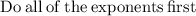
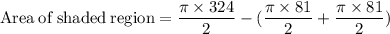
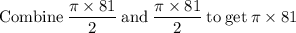
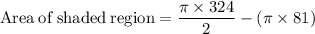
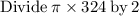
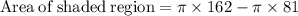
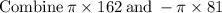
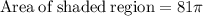
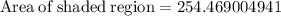
Area of shaded region rounded to the nearest tenth is: 254.5 square units
look at the picture for more information